Tidal disruption events (TDEs) are one of the most dramatic multi-messenger transients in which a star, that happens to orbit so close to a supermassive black hole, is tidally disrupted by the black hole in a few hours, generating a flare luminous enough to outshine the entire host galaxy.

1. Tidal disruption radius

One of the most important key factors for TDEs is the characteristic closest-approach distance, which is known as “tidal disruption radius”. The expression for the tidal disruption radius can be derived by equating the two forces, the black hole’s tidal force GM_{\mathrm{BH}}R_{\star}/R^{3} and the star’s self-gravity GM_{\star}/R_{\star}^{2}, both at the stellar surface, which gives,

    \[ r_{\mathrm{t}} = \left(\frac{M_{\mathrm{BH}}}{M_{\star}}\right)^{1/3}R_{\star}, \]

where M_{\mathrm{BH}} is the black hole mass, M_{\star} the stellar mass, and R_{\star} the stellar radius.

We can consider two asymptotic values of r_{\mathrm{t}}. First, as M_{\mathrm{BH}} decreases, r_{\mathrm{t}} approaches R_{\star}, but becomes greater than the event horizon of the black hole (r_{\mathrm{t}}/r_{\mathrm{g}}\sim O(10^{4}-10^{5}) for stellar-mass black holes). The latter means that relativistic effects become less important. On the other hand, as M_{\mathrm{BH}} increases, r_{\mathrm{t}}/r_{\mathrm{g}} drops, meaning that relativistic effects become more important. Here, we can define the maximum black hole mass M_{\mathrm{max,BH}} capable of disrupting stars outside of the event horizon or M_{\mathrm{max,BH}} for which r_{\mathrm{t}}\leq\alpha r_{\mathrm{ g}},

(1)   \begin{align*} M_{\mathrm{max,BH}}\gtrsim 10^{8}\mathrm{M}_{\odot}\left(\frac{2}{\alpha}\right)^{3/2}\left(\frac{\mathrm{M}_{\star}}{1\mathrm{M}_{\odot}}\right)^{-1/2} \left(\frac{R_{\star}}{1\mathrm{R}_{\odot}}\right)^{3/2}. \end{align*}

A star on Schwarzschild geodesic falling from infinity with orbital angular momentum L\leq4r_{\mathrm{ g}}c (corresponding to \alpha=4) would directly fall into the SMBH without generating any flares. Notice that the relativistic angular momentum L in Schwarzschild space time for the parabolic case is expressed as,

(2)   \begin{align*} L^{2}=(r_{\mathrm{g}}c)^{2}\frac{2(r_{\mathrm{p}}/r_{\mathrm{ g}})^{2}}{r_{\mathrm{ p}}/r_{\mathrm{ g}}-2}. \end{align*}

}.

Let’s step back and think about how we derive r_{\mathrm{t}}. We have derived the expression for r_{\mathrm{t}} by comparing the order-of-magnitude estimates for the two forces at the stellar surface. As a result, r_{\mathrm{t}}\propto\bar{\rho}_{\star}^{-1/3} where \bar{\rho}_{\star}\equiv M_{\star}/[4\pi R_{\star}^{3}/3] is the average density of the star. Comparing the two forces at the stellar surface makes r_{\mathrm{t}} an approximate estimate for the maximum pericenter distance at which the star loses some mass during the pericenter passage and survives (partial disruption events). Full disruptions occur only when the tidal force is greater than the self-gravity at the densest region of the star, i.e., its core. Then it naturally follows that the maximum pericenter distance for full disruptions \mathcal{R}_{\mathrm{t}} should be more related to the core structure, especially the central density \rho_{\mathrm{c}}, or,

(3)   \begin{align*} \mathcal{R}_{\mathrm{t}}\simeq\left(\frac{M_{\mathrm{BH}}}{\rho_{\mathrm{c}}}\right)^{1/3}. \end{align*}

See Section 4 of Ryu et al. 2020 for the full derivation of this expression.

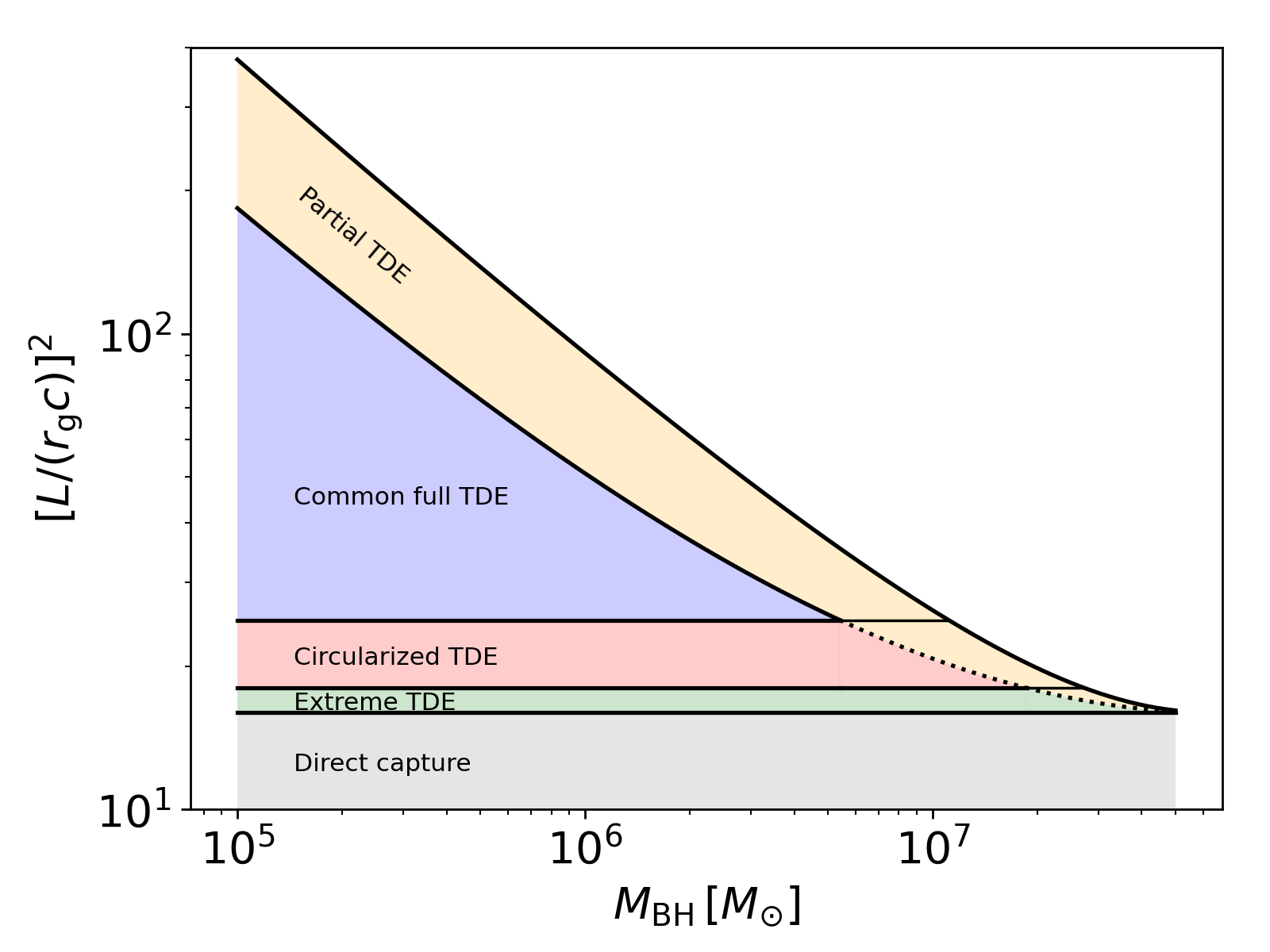
2. Varieties of Tidal Disruption Events

TDEs may be categorized into five groups:

2.1) partial TDE
2.2) common full TDE
2.3) circularized full TDE
2.4) extreme TDE, and
2.5) direct capture.

The figure below shows the range of L^2 for each group, as a function of black hole mass. Here, L is the relativistic angular momentum (see Equation 2). Note that the encounter cross-section is proportional to L^2. So the ratio of L^2 for each type of TDEs gives the relative encounter probability.

reference: Ryu, Krolik, Piran, ApJ 946, 33 (2023)

2-1. Partial Tidal Disruption Event

Partial tidal disruption events (PTDEs) are the events where stars survive during the pericenter passage after losing some mass. The outcomes of PTDEs are a remnant and stellar debris. Both of them can create unique observational signatures.

  • Remnant
    This video shows a PTDE of a 3Msol main-sequence star by 4 million Msol black hole.

    The remnant has interesting features upon disruption. It is hotter than the ordinary star of the same mass, spun-up in the prograde direction, undergoes violent chemical mixing. This features suggest that the remnant can reveal unique observational signatures even when it settles to a stable state.

  • Debris
    Like full TDEs, bound debris returns to the black hole, generating a flare. If the remnant is bound and undergoes a PTDE multiple times, repeated electromagnetic flares are possible (see Ryu et al. 2020).
2-2 and 2-3. Full Disruption Event – common vs circularized

One of the long-standing problems in TDEs is what powers optical/UV bright TDEs. There have been two competing mechanisms. In “rapid circularization” scenario, if relativistic apsidal precession is strong, returned debris turns around the black hole with a large apsidal precession angle and collide with newly returning debris near pericenter. The collision create shocks, which dissipate the orbital energy efficiently. The debris circularizes quickly and forms a compact accretion disk. The main energy source in this scenario is energy liberated in accretion. In the second scenario, because apsidal precession in most TDEs is not strong, stream-stream collisions occur farther out near apocenter of the debris. It also creates shocks, which dissipates the orbital energy. But the dissipation is not efficient enough for the debris to circularize rapidly. The outcome is an extended eccentric outflow. The main energy source is the energy dissipated by the apocenter shock, which is radiated.

The only way to study which mechanism is dominant is perform global relativistic simulations of TDEs with realistic initial conditions. My collaborators and I are actually doing that!

See the movies from the first relativistic global simulation for a TDE of a 3 solar mass main-sequence star by a 100000 solar mass black hole.

– Evolution near the first pericenter passage

– Evolution after the first pericenter passage

I am also very enthusiastic about outreach activities. See this Youtube Clip, made with NASA using my simulations, live-streamed on Black hole Friday!

(https://www.nasa.gov/feature/goddard/2021/scientists-fling-model-stars-at-a-virtual-black-hole-to-see-who-survives)

2-4. Extreme Tidal Disruption Event

If the tidal radius is slightly greater than the event horizon, tidal disruptoin events become very relativistic. For this case, following the stellar orbit, the debris is initially distributed in a crescent, it then turns into a set of tight spirals circling the black hole, which merge into a shell expanding radially outwards. Some mass later falls back toward the black hole, while the remainder is ejected. Internal shocks within the infalling debris power the observed emission. The resulting lightcurve rises rapidly to roughly the Eddington luminosity, maintains this level for between a few weeks and a year (depending on both the stellar mass and the black hole mass), and then drops. Most of its power is in thermal X-rays at a temperature ~(1-2) × 106 K (~100-200 eV). The debris evolution and observational features of extreme TDE (or eTDE) are qualitatively different from ordinary TDEs, making eTDEs a new type of TDE. Although eTDEs are relatively rare for lower-mass black holes, most tidal disruptions around higher-mass black holes are extreme. Their detection offers a view of an exotic relativistic phenomenon previously inaccessible.

See this movie showing how a star is destroyed in an eTDE.

2-5. Direct Capture Event

When the pericenter distance of a parabolic orbit is less than 4 r_{mathrm{g}} (or L<4 r_{mathrm{g}}c), the star would be swallowed whole without generating significant electromagnetic radiation. See this movie from a fully relativistic hydrodynamics simulation!